一个很有趣的模型,适用于有限状态的的预测。下周搞完辅导的预测看看是怎么整股市的HMM预测的。
- 有限状态序列Q
- 有限观测系列T
马尔科夫
俄国数学家安德烈·马尔可夫(俄语:Андрей Андреевич Марков)提出。
第一次了解到马尔科夫这个概念,是16年的《随机信号分析课堂》上,应该是用于描述信号传输过程中信号,其中有限状态机、生成概率、转移概率之类的概念,也是在课上了解,不过当时听得云里雾里(主要是上课没认真,是真的遗憾),只记得老师讲的段子了:同学们现在课堂上睡不睡觉,并不取决于昨天晚上睡得好不好,而是取决于前一秒同学们想不想睡。
不过马尔科夫的基本思想就是这样:下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关(无记忆性)。这种特定类型的“无记忆性”称作马尔可夫性质。
在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做转移,与不同的状态改变相关的概率叫做转移概率。
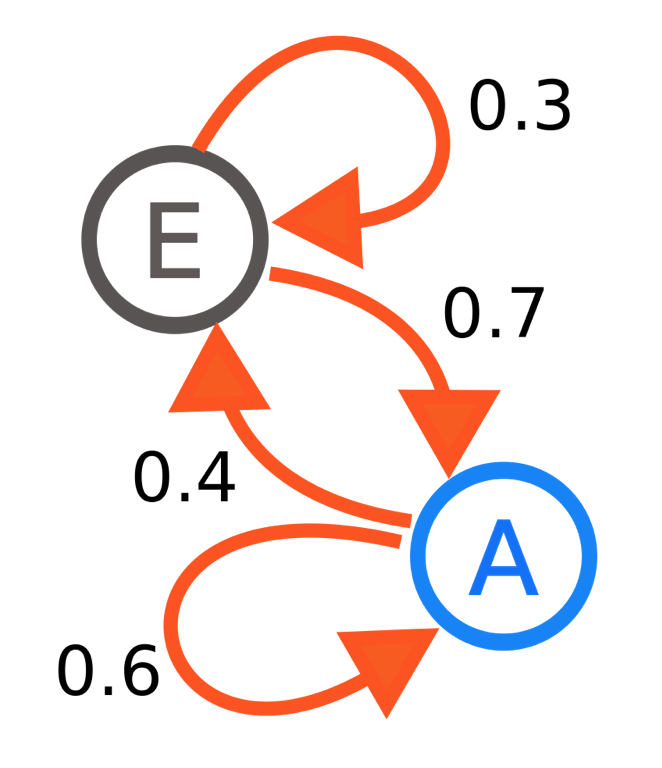
隐马尔科夫
写在最前
这篇文章绝大部分内容来自互联网,只是自己跟着完全走了一遍并加入了一下自己的心得想法。
隐马尔可夫模型,简称HMM(Hidden Markov Model), 是一种基于概率的统计分析模型,用来描述一个系统隐性状态的转移和隐性状态的表现概率。
举个栗子
假设我们有三个完全正常的骰子,分别是四面体D4,六面体D6,八面体D8(那么其每一面出现的概率分别是1/4,1/6,1/8):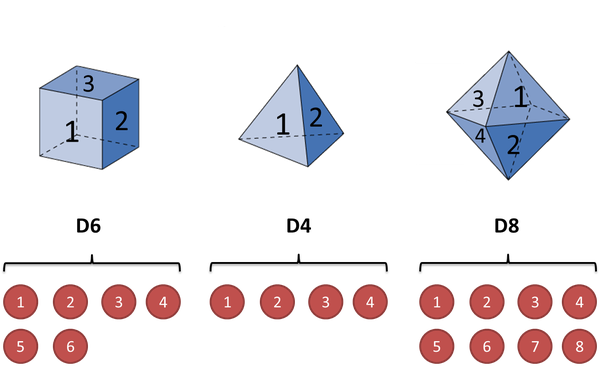
然后我们就可以开始至骰子了:
- 任意条一个骰子(每一个被挑中的概率是1/3)
- 掷骰子(出现1-8之间的数字)
然后我们不同重复上述过程,即可得到一串数字(假设投十次):1 6 3 5 2 7 3 5 2 4
我们称这串数字是可见状态链
当然我们今天要介绍的模型是隐马尔科夫模型,当然不会这么简单,其中还存在这一串隐含状态链,即在这里例子中可能是D6 D8 D8 D6 D4 D8 D6 D6 D4 D8或者其他的隐含状态链。
一般我们在HMM中的马尔可夫链指的应该是隐含状态链,因为其存在这转化概率(即我们挑骰子过程中选择哪一个骰子),而可见状态是有隐含状态决定的,并不存在直接的转化概率。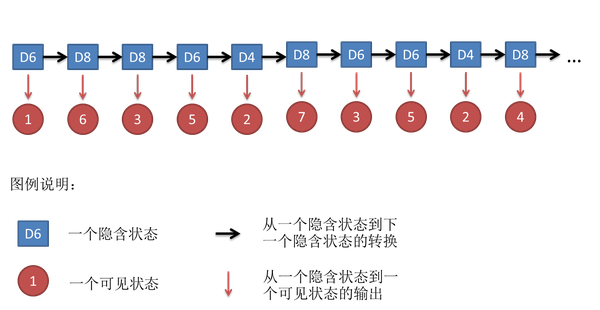
在这个例子里,D6的下一个状态是D4,D6,D8的概率都是1/3。D4,D8的下一个状态是D4,D6,D8的转换概率也都一样是1/3。我们其实可以随意设定转换概率的。比如,我们可以这样定义:D6后面不能接D4,D6后面是D6的概率是0.9,是D8的概率是0.1。这样就是一个新的HMM。
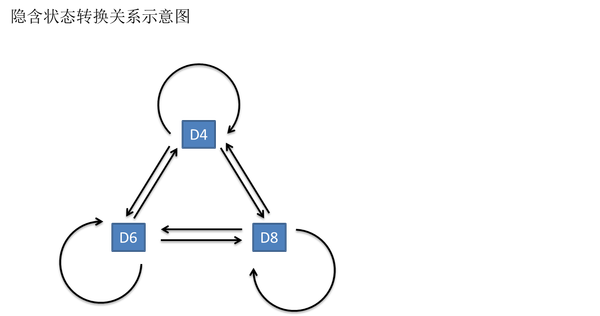
前面我们说道马尔可夫链存在转化概率,且可见转态链没有,但是隐含状态与可见状态存在这输出概率,这个例子里面挺简单即D4:1/4 D6:1/6 D8:1/8当然也可以不是这个,加入赌场做点手脚不就变了嘛。
其实对于HMM来说,如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率,做模拟是相当容易的。但在实际运用中,往往会缺失一部分信息:有时候你知道骰子有几种,每种骰子是什么,但是不知道掷出来的骰子序列;有时候你知道骰子序列,剩下的什么都不知道。
主要解决这三类问题
- 知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次掷出来的都是哪种骰子(隐含状态链)。
- 还是知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。
- 知道骰子有几种(隐含状态数量),不知道每种骰子是什么(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种骰子是什么(转换概率)
来玩骰子吧
假设我们给出下图所示的概率,求出现此序列的概率P: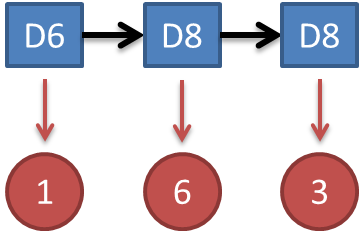
很简单可以这么算:
现在我们看第一个问题,知道我有D4、D6、D8三个骰子(即知道隐含状态),也知道可见状态序列(1 6 3 5 2 7 3 5 2 4),现在我想知道每次投出来的都是哪些骰子(解最大似然路径问题,假设每个包含当前可见状态的骰子被选中的概率相等)。这个问题是可以通过穷举的方式去解决的,即像上面一样去计算骰子组合的出现的概率,然后选择其中概率最大就OK,但是会出现计算量过大的问题(指数级增大)。
一般解决这种问题的方式是采用维特比算法,通过DP思想去解决这个问题,当然这方面可以说的东西太多了…根本不是这里可以说清楚的,大学时《信息编码》这么课有使用这个算法去解码,当时觉得这个算法没啥用,现在真的被啪啪打脸!这里借用《数学之美》里面的一个京深铁路最短路径的问题一下解释。
中国现在铁路网四通八达,打开12306就可以知道从北京去往深圳的铁路可以有很多种出行组合方式(石家庄郑州武汉上海等节点),现在不考虑时间问题,怎么走才是公里数最短的呢?
我们可以这样假设,即必然存在一条路径使得京深最短。现在先反推,我们可以知道如果我们从深圳回溯到其上一站A,则北京到A的公里数必然为最短的,不然我们的假设不成立。以此类推,我们在此路径上的任意一个节点,北京到其的距离也必然是最短的。
那么现在从正面开始看,即只要找到北京出发到每个层级节点的最优路径就好了(层级节点就是划分把全局最优化解为局部最优的重点)
现在要做的话只需要搞一下基本就好了
- 从序列长度为1算起,算序列长度为1时取到每个骰子的最大概率
- 然后,逐渐增加长度,每增加一次长度,重新算一遍在这个长度下最后一个位置取到每个骰子的最大概率。因为上一个长度下的取到每个骰子的最大概率都算过了,重新计算的话其实不难。当我们算到最后一位时,就知道最后一位是哪个骰子的概率最大了。
- 推出序列
HMM应用必要条件
- 隐性状态的转移必须满足马尔可夫性(二元或N元)
- 隐性状态必须能够大概被估计
HMM适用的问题:真正的状态(隐态)难以被估计,而状态与状态之间又存在联系
具体应用场景
《数学之美》里面讲了一些例子,列一列
- 语音识别
- 中文分词
- 拼音输入
- 手写输入
- 股市预测
- …