Posted on

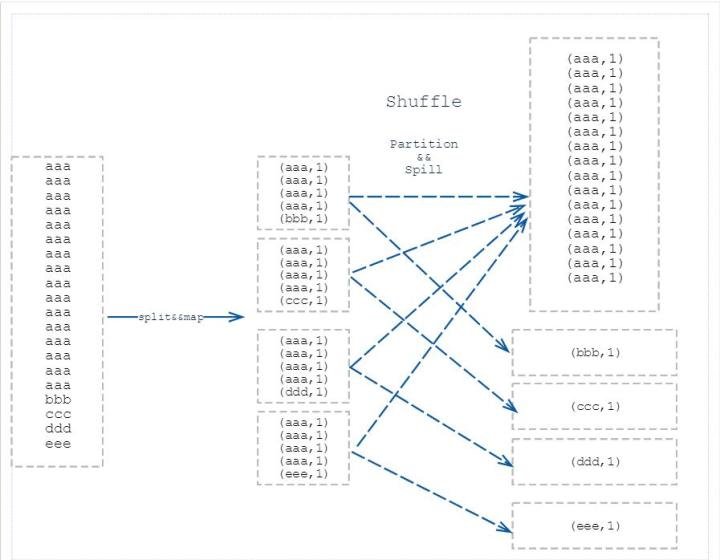
SerDe是Serialize/Deserialize的简称，即序列化和和反序列化

序列化的作用

  • 序列化是对象转化为字节序列的过程 

    1
    Row object --> Serializer --> <key, value> --> OutputFileFormat --> HDFS files

  • 反序列化是字节序列恢复为对象的过程

    1
    HDFS files --> InputFileFormat --> <key, value> --> Deserializer --> Row object

  • 我们对对象序列化主要用于：

    • 对象的持久化
    • 对象的网络传送

Hive的反序列化是吧k-v数据反序列化成为Table里的列值，而不需要转化，为海量数据处理节省大量时间。

SerDe说明hive如何去处理一条记录，包括Serialize/Deserilize两个功能， Serialize把hive使用的java object转换成能写入hdfs的字节序列，或者其他系统能识别的流文件。Deserilize把字符串或者二进制流转换成hive能识别的java object对象。比如：select语句会用到Deserialize对象， 把hdfs数据解析出来；insert语句会使用Serilize，数据写入hdfs系统，需要把数据序列化。

SerDe的使用

Hive建表的时候可以使用自定义的SerDe或者Hive内置的SerDe类型指定数据的序列化和反序列化的方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
--指定*.RequestSerde做Serde

create table xxx
(
 userid  string ,
 nickname string ,
 xxx and so on 
)

PARTITIONED BY (
  `year` string,
  `month` string,
  `day` string)
ROW FORMAT SERDE
  'com.fenbi.ape.hive.serde.RequestSerde'
STORED AS INPUTFORMAT
  'org.apache.hadoop.mapred.TextInputFormat'
OUTPUTFORMAT
  'org.apache.hadoop.hive.ql.io.HiveIgnoreKeyTextOutputFormat'
LOCATION
  'hdfs://f04/log/tutor'

SerDe内置类型

  • Avro
  • ORC
  • RegEx
  • ThrifT
  • Parquet
  • CSV
  • JsonSerDe

自定义类型

定义一个类，继承抽象类AbstractSerDe

1
2
2018-10-18
demo code to be added

Posted on

写在最前

Markdown写东西是很舒服，不过难免会有用到数学公式的地方，之前的解决方式是在Word或者在线编辑器上写好，然后生成图片贴到文章上，这样缺点其实蛮多的（难以修改，格式混乱），现在有了MathJax这样的利器，今晚就跟着大神的博客自己走一遍！

使用参考

如何插入公式

  • 行中公式(放在文中与其它文字混编)可以用$来标记
  • 独立公式可以用两个$来标记
  • 自动编号公式：在每个公式末尾前使用\tag{行标}
1
我们常说的欧拉公式$e^{i\pi}+1=0$

显示：
我们常说的欧拉公式$e^{i\pi}+1=0$

1
$$ e^{i\pi}+1=0 $$

显示：

输入上下标

^表示商标，_表示下标，两者可以同时使用，也可以嵌套。如果遇到多个字符组成组成的内容，可以使用{}来表示为一个整体。

1
$$ e^{x^\pi}=1+y^z $$

结果显示:

如何输入括号和分隔符

()、|还有[]都表示本身{需要使用\转义，即\{\}表示{},可以用\left和\right命令表示大括号或分隔符。

1
$$f(x,y,z)=e^{xz}+2x\left(3+\frac{1+x}{1+xyz}\right)$$

显示：

如何输入分数

利用\frac{}{}来表示，可以嵌套；使用\frac ab快速生成；分子 \over 分母可表示只有一层的分母

1
$$ \frac {a+1}{b-1} \quad and \quad \frac {a-1}b \quad and \quad {a-1 \over b+1}  $$

显示：

如何输入开方

\sqrt [根指数，省略时为2] {被开方数}表示开方

1
$$\sqrt [3] {xyz}  \quad and \quad \sqrt {x}$$

显示：

如何输入省略号

数学公式中常见的省略号有两种,\ldots表示与文本底线对齐的省略号,\cdots表示与文本中线对齐的省略号。

1
$$P(w_1,w_2,\cdots,w_n|y_1,y_2,\cdots,y_n)=\frac{P(y_1,y_2,\cdots,y_n|w_1,w_2,\cdots,w_n)P(w_1,w_2,\cdots,w_n)}{P(y_1,y_2,\cdots,y_n)}$$

显示：

如何输入矢量

\vec{矢量}来表示一个矢量

1
$$ \vec{a} \cdot \vec{c} = 0 $$

显示：

如何输入积分

\int_积分下限^积分上限 {被积表达式}表示一个积分

1
$$\int^a_b{x^2}\,{\rm d}x = {1 \over 3}(a^3-b^3)$$

显示：

如何输入极限运算

使用\lim_{变量 \to 表达式}来表示极限，\infty表示取极限，前面可加正负号。

1
$$\lim_{n \to +\infty} {1 \over 1+e^{-n}}=1$$

显示

如何表示累积运算

使用\sum_{下标表达式}^{上标表达式}{}表示累加。
与之类似，使用\prod，\bigcup，\bigcap来分别输入累乘、并集和交集

1
$$\frac{\pi}{4} = \sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}$$

显示：

怎么输入希腊字母

输入\小写希腊字母英文全称和\首字母大写希腊字母英文全称来分别输入小写和大写希腊字母。
对于大写希腊字母与现有字母相同的，直接输入大写字母即可。

输入 显示 输入 显示
\alpha $\alpha$ A $A$
\beta $\beta$ B $B$
\gamma $\gamma$ \Gamma $\Gamma$
\delta $\delta$ \Delta $\delta$
\epsilon $\epsilon$ E $E$
\zeta $\zeta$ Z $Z$
\eta $\eta$ H $H$
\theta $\theta$ \Theta $\Theta$
\iota $\iota$ I $I$
\kappa $\kappa$ K $K$
\lambda $\lambda$ \Lambda $\Lambda$
\nu $\nu$ N $N$
\mu $\mu$ M $M$
\xi $\xi$ \Xi $\Xi$
o $o$ O $O$
\pi $\pi$ \Pi $\Pi$
\rho $\rho$ P $P$
\sigma $\sigma$ \Sigma $\Sigma$
\tau $\tau$ T $T$
\upsilon $\upsilon$ \Upsilon $\Upsilon$
\phi $\phi$ \Phi $\Phi$
\chi $\chi$ X $X$
\psi $\psi$ \Psi $\Psi$
\omega $\omega$ \Omega $\Omega$

大括号和行标的使用

使用\left和\right来创建自动匹配高度的 (圆括号)，[方括号] 和 {花括号} 。
在每个公式末尾前使用\tag{行标}来实现行标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
$$
f\left(
   \left[ 
     \frac{
       1+y
     }{
       \left(
          \frac{x}{y}+\frac{y}{x}
       \right)
       \left(u+1\right)
     }+a
   \right]^{3/2}
\right)
\tag{行标}
$$

特殊函数

1
$$  \sinx \quad and \quand \lnx \quad and \quad \max(a,b,c)  $$

显示：

矩阵展示

基本语法

起始标记\begin{matrix}，结束标记\end{matrix}
每一行末尾标记\\\，行间元素之间以&分隔

1
2
3
4
5
$$\begin{matrix}
1&0&1\\\
0&1&1\\\
0&1&0\\\
\end{matrix}$$

显示：

矩阵边框

在起始、结束标记处用下列词替换 matrix

  • pmatrix ：小括号边框
  • bmatrix ：中括号边框
  • Bmatrix ：大括号边框
  • vmatrix ：单竖线边框
  • Vmatrix ：双竖线边框
    1
    2
    3
    4
    5
    $$\begin{matrix}
    1&0&1\\\
    0&1&1\\\
    0&1&0\\\
    \end{matrix}$$

显示：

省略元素

同上，添加\vdots代表斜省略号

方程组

case环境。

1
2
3
4
5
6
$$\begin{cases}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3\\
\end{cases}
$$

显示：

赶紧睡觉！！！

Posted on

一个很有趣的模型，适用于有限状态的的预测。下周搞完辅导的预测看看是怎么整股市的HMM预测的。

  • 有限状态序列Q
  • 有限观测系列T

马尔科夫

俄国数学家安德烈·马尔可夫（俄语：Андрей Андреевич Марков）提出。

第一次了解到马尔科夫这个概念，是16年的《随机信号分析课堂》上，应该是用于描述信号传输过程中信号，其中有限状态机、生成概率、转移概率之类的概念，也是在课上了解，不过当时听得云里雾里（主要是上课没认真，是真的遗憾），只记得老师讲的段子了：同学们现在课堂上睡不睡觉，并不取决于昨天晚上睡得好不好，而是取决于前一秒同学们想不想睡。

不过马尔科夫的基本思想就是这样：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关（无记忆性）。这种特定类型的“无记忆性”称作马尔可夫性质。

在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态。状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率。

隐马尔科夫

写在最前

这篇文章绝大部分内容来自互联网，只是自己跟着完全走了一遍并加入了一下自己的心得想法。

隐马尔可夫模型，简称HMM(Hidden Markov Model), 是一种基于概率的统计分析模型，用来描述一个系统隐性状态的转移和隐性状态的表现概率。

举个栗子

假设我们有三个完全正常的骰子，分别是四面体D4，六面体D6，八面体D8（那么其每一面出现的概率分别是1/4,1/6,1/8）:

然后我们就可以开始至骰子了：

  • 任意条一个骰子（每一个被挑中的概率是1/3）
  • 掷骰子（出现1-8之间的数字）
    然后我们不同重复上述过程，即可得到一串数字（假设投十次）：
    1 6 3 5 2 7 3 5 2 4
    我们称这串数字是可见状态链

当然我们今天要介绍的模型是隐马尔科夫模型，当然不会这么简单，其中还存在这一串隐含状态链，即在这里例子中可能是D6 D8 D8 D6 D4 D8 D6 D6 D4 D8或者其他的隐含状态链。

一般我们在HMM中的马尔可夫链指的应该是隐含状态链，因为其存在这转化概率（即我们挑骰子过程中选择哪一个骰子），而可见状态是有隐含状态决定的，并不存在直接的转化概率。

在这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。我们其实可以随意设定转换概率的。比如，我们可以这样定义：D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

前面我们说道马尔可夫链存在转化概率，且可见转态链没有，但是隐含状态与可见状态存在这输出概率，这个例子里面挺简单即D4:1/4 D6:1/6 D8:1/8当然也可以不是这个，加入赌场做点手脚不就变了嘛。

其实对于HMM来说，如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率，做模拟是相当容易的。但在实际运用中，往往会缺失一部分信息：有时候你知道骰子有几种，每种骰子是什么，但是不知道掷出来的骰子序列；有时候你知道骰子序列，剩下的什么都不知道。

主要解决这三类问题

  • 知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道每次掷出来的都是哪种骰子（隐含状态链）。
  • 还是知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。
  • 知道骰子有几种（隐含状态数量），不知道每种骰子是什么（转换概率），观测到很多次掷骰子的结果（可见状态链），我想反推出每种骰子是什么（转换概率）

来玩骰子吧

假设我们给出下图所示的概率，求出现此序列的概率P:

很简单可以这么算：

现在我们看第一个问题，知道我有D4、D6、D8三个骰子（即知道隐含状态），也知道可见状态序列(1 6 3 5 2 7 3 5 2 4)，现在我想知道每次投出来的都是哪些骰子（解最大似然路径问题，假设每个包含当前可见状态的骰子被选中的概率相等）。这个问题是可以通过穷举的方式去解决的，即像上面一样去计算骰子组合的出现的概率，然后选择其中概率最大就OK，但是会出现计算量过大的问题（指数级增大）。

一般解决这种问题的方式是采用维特比算法，通过DP思想去解决这个问题，当然这方面可以说的东西太多了…根本不是这里可以说清楚的，大学时《信息编码》这么课有使用这个算法去解码，当时觉得这个算法没啥用，现在真的被啪啪打脸！这里借用《数学之美》里面的一个京深铁路最短路径的问题一下解释。

中国现在铁路网四通八达，打开12306就可以知道从北京去往深圳的铁路可以有很多种出行组合方式（石家庄郑州武汉上海等节点），现在不考虑时间问题，怎么走才是公里数最短的呢？
我们可以这样假设，即必然存在一条路径使得京深最短。现在先反推，我们可以知道如果我们从深圳回溯到其上一站A，则北京到A的公里数必然为最短的，不然我们的假设不成立。以此类推，我们在此路径上的任意一个节点，北京到其的距离也必然是最短的。
那么现在从正面开始看，即只要找到北京出发到每个层级节点的最优路径就好了（层级节点就是划分把全局最优化解为局部最优的重点）

现在要做的话只需要搞一下基本就好了

  • 从序列长度为1算起，算序列长度为1时取到每个骰子的最大概率
  • 然后，逐渐增加长度，每增加一次长度，重新算一遍在这个长度下最后一个位置取到每个骰子的最大概率。因为上一个长度下的取到每个骰子的最大概率都算过了，重新计算的话其实不难。当我们算到最后一位时，就知道最后一位是哪个骰子的概率最大了。
  • 推出序列

HMM应用必要条件

  • 隐性状态的转移必须满足马尔可夫性（二元或N元）
  • 隐性状态必须能够大概被估计

HMM适用的问题：真正的状态(隐态)难以被估计，而状态与状态之间又存在联系

具体应用场景

《数学之美》里面讲了一些例子，列一列

  • 语音识别
  • 中文分词
  • 拼音输入
  • 手写输入
  • 股市预测
  • …

Posted on

什么是数据倾斜

最直白的语句来看数据倾斜就是数据里某一个key的值太多了，导致task处理其的时间远远超过其他任务，hadoop的常见现象就是任务卡在99%,迟迟不结束。我觉得可以理解为木桶原理，因为运行最慢的task拖慢了整个任务的运行时间。

不过也可以这么解释：数据倾斜就是我们在计算数据的时候，数据的分散度不够，导致大量的数据集中到了一台或者几台机器上计算，这些数据的计算速度远远低于平均计算速度，导致整个计算过程过慢。

一般表现为某个任务Reduce阶段卡在99%不动，以及随之而来的种种诡异现象。

数据倾斜的问题并不是随着节点的增多而解决的，比如看个例子：

  • 公司 A : 1000万用户，10台64G服务器
  • 公司 B : 10亿用户，1000台64G服务器

两个公司都部署了Hadoop集群。假设现在遇到了数据倾斜，发生什么？

公司A的数据童鞋在做join的时候发生了数据倾斜，会导致有几百万用户的相关数据集中到了一台服务器上，几百万的用户数据，感觉64G还是轻松的。

公司B的数据童鞋在做join的时候也发生了数据倾斜，可能会有1个亿的用户相关数据集中到了一台机器上了，一台机器估计就很难搞了，整个task会因为这个而卡住。

数据倾斜的原理

数据倾斜产生的原因

我们在做数据运算的时候，肯定会使用到count,distinct,group by,join/等操作，这些都会触发Shuffle操作，一但出现Shuffle过程中天量相同Key值的数据拉到一个或者少数几个节点上，就容易踩坑。。。

Shuffle

Shuffle过程在Hadoop或者Spark中都是至关重要的，产生的原因也很清晰明了，如下图所示
shuffle过程

比如说
  • 两个开发同学分别设计了user(userid,ip)表和ip_log(ip,logtime)表，其中user.ip的值如果获取不到的话，则默认为null，对于获取不到ip的用户，则取ip_log.ip=0，在这样的情况下，当两个表做join操作的时候，就很有可能卡住（空值由一个reduce处理）
  • 业务上搞了大事，单个城市订单猛涨1000倍之类的。

常见情况参见:

关键词 情形 后果
join 其中一个表较小，但是key集中 分发到某一个或几个Reduce上的数据远高于平均值
join 大表与大表，但是分桶的判断字段0值或空值过多 一个reduce处理，极其慢
group by group by维度过小，导致某值的数量过多 某reduce耗时久
count distinct 某特殊值过多 某reduce耗时久

数据倾斜解决

SQL调优
  • join数据量太大的时候，可以考虑先distinct去重
  • 大表Join大表，把空值的key变成一个字符串加上随机数，把倾斜的数据分到不同的reduce上，由于null值关联不上，处理后并不影响最终结果。（先对key做一层hash，先将数据打散让它的并行度变大，再汇集）
  • join 操作中，使用 map join 在 map 端就先进行 join ，免得到reduce 时卡住
  • 能先进行 group 操作的时候先进行 group 操作，把 key 先进行一次 reduce,之后再进行 count 或者 distinct count 操作。
  • 特殊情况特殊处理，在业务逻辑优化效果的不大情况下，有些时候是可以将倾斜的数据单独拿出来处理。最后union回去。
参数调优
  • set hive.map.aggr=true:在map中会做部分聚集操作，效率更高但需要更多的内存
  • hive.groupby.skewindata=true：数据倾斜时负载均衡，当选项设定为true，生成的查询计划会有两个MRJob。第一个MRJob 中，Map的输出结果集合会随机分布到Reduce中，每个Reduce做部分聚合操作，并输出结果，这样处理的结果是相同的GroupBy Key有可能被分发到不同的Reduce中，从而达到负载均衡的目的；第二个MRJob再根据预处理的数据结果按照GroupBy Key分布到Reduce中（这个过程可以保证相同的GroupBy Key被分布到同一个Reduce中），最后完成最终的聚合操作。
  • hive.auto.convert.join=true:自动开启mapjoin优化
  • 未完待续

Posted on

xbb

Hive查询使用中难免遇到各种各样奇奇怪怪的需求或者角度，这个时候合理使用分析窗口函数也许会有很好的效果

前面《我的Hive学习之旅》一文主要讲了row_number(),动态group by还有日期处理之类的问题，稍微涉及了一些窗口函数的东西，但是并没有较为详细地整理一下。今天有时间就整理一下吧~

窗口函数：

窗口函数 描述
lead 用于统计窗口内往下第n行值。
lag 与lead相反，用于统计窗口内往上第n行值。
first_value 取分组排序后，截止到当前行，第一个值
last_value 取分组排序后，截止到当前行，最后一个值

分析函数：

分析函数 描述
RANK 返回数据项在分区中的排名。排名值序列可能会有间隔
DENSE_RANK 返回数据项在分区中的排名。排名值序列是连续的，不会有间隔
PERCENT_RANK 计算当前行的百分比排名
ROW_NUMBER 确定分区中当前行的序号
CUME_DIST 计算分区中当前行的相对排名
NTILE() 将每个分区的行尽可能均匀地划分为指定数量的分组

over子句

  • OVER子句可以与标准聚合函数使用(COUNT，SUM，MIN，MAX，AVG)
  • OVER可以与一个或多个任何原始数据类型的分区列的PARTITION BY语句使用。
  • OVER可以与一个或多个任何原始类型的分区列（排序列）的PARTITION BY(ORDER BY)使用。
  • 带有窗口规范的OVER子句。窗口可以在WINDOW子句中单独定义。 窗口规范支持如下格式
    1
    2
    3
    4
    5
    6
    7
    8
    9

    (ROWS | RANGE) BETWEEN (UNBOUNDED | [num]) PRECEDING AND ([num] PRECEDING | CURRENT ROW | (UNBOUNDED | [num]) FOLLOWING)
    (ROWS | RANGE) BETWEEN CURRENT ROW AND (CURRENT ROW | (UNBOUNDED | [num]) FOLLOWING)
    (ROWS | RANGE) BETWEEN [num] FOLLOWING AND (UNBOUNDED | [num]) FOLLOWING

    eg:
    select dt , count(userid) over day_window as user_num
    from table
    window day_window as (partition by userid,dt  order by diffdays ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW )

当缺少WINDOW子句并指定使用ORDER BY时，窗口规范默认为RANGE BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW，即从第一行到当前行。

当缺少ORDER BY和WINDOW子句时，窗口规范默认为ROW BETWEEN UNBOUNDED PRECEDING AND UNBOUNDED FOLLOWING，即第一行到最后一行。

备注

PRECEDING：表示当前行之前的行

UNBOUNDED PRECEDING： 第一行

num PRECEDING：当前行之前的第num行

CURRENT ROW：当前行

FOLLOWING：当前行之后的行

UNBOUNDED FOLLOWING：最后一行

num FOLLOWING：当前行之后的第num行

range是逻辑窗口，是指定当前行对应值的范围取值，列数不固定，只要行值在范围内，对应列都包含在内

rows是物理窗口，即根据order by 子句排序后，取的前N行及后N行的数据计算（与当前行的值无关，只与排序后的行号相关）

示例代码中便是在带有窗口规范的OVER子句，其窗口便在window子句中单独定义，但如果是分析规范，则不支持。

小提示

在count()等聚合函数中，distinct在hive2.2.0之后才支持order by子句和窗口规范
hive2.1.0之后over子句中支持聚合函数

实战演习

分组取top n

row_number()搭配over子句安排得很明明白白，还有xx_rank()几个函数供使用

1
2
3
4
select seasonid, episodeid , 
row_number() over(partition by seasonid order by episodeid asc) as rank 
from tutor.dw_season_live_information a 
where dt = date_sub(current_date,1)

计算累计

引用网上数据

1
2
3
4
5
6
7
8
9
10

hive> select * from lxw1234;
OK
cookie1 2015-04-10      1
cookie1 2015-04-11      5
cookie1 2015-04-12      7
cookie1 2015-04-13      3
cookie1 2015-04-14      2
cookie1 2015-04-15      4
cookie1 2015-04-16      4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
SELECT cookieid,
createtime,
pv,
SUM(pv) OVER(PARTITION BY cookieid ORDER BY createtime) AS pv1, -- 默认为从起点到当前行
SUM(pv) OVER(PARTITION BY cookieid ORDER BY createtime ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) AS pv2, --从起点到当前行，结果同pv1 
SUM(pv) OVER(PARTITION BY cookieid) AS pv3,	--分组内所有行
SUM(pv) OVER(PARTITION BY cookieid ORDER BY createtime ROWS BETWEEN 3 PRECEDING AND CURRENT ROW) AS pv4,  --当前行+往前3行
SUM(pv) OVER(PARTITION BY cookieid ORDER BY createtime ROWS BETWEEN 3 PRECEDING AND 1 FOLLOWING) AS pv5,  --当前行+往前3行+往后1行
SUM(pv) OVER(PARTITION BY cookieid ORDER BY createtime ROWS BETWEEN CURRENT ROW AND UNBOUNDED FOLLOWING) AS pv6  ---当前行+往后所有行  
FROM lxw1234;
 
cookieid createtime     pv      pv1     pv2     pv3     pv4     pv5      pv6 
-----------------------------------------------------------------------------
cookie1  2015-04-10      1       1       1       26      1       6       26
cookie1  2015-04-11      5       6       6       26      6       13      25
cookie1  2015-04-12      7       13      13      26      13      16      20
cookie1  2015-04-13      3       16      16      26      16      18      13
cookie1  2015-04-14      2       18      18      26      17      21      10
cookie1  2015-04-15      4       22      22      26      16      20      8
cookie1  2015-04-16      4       26      26      26      13      13      4

时间序列分析

主要使用lead()等函数

Posted on

2018-11-19

有这样的友谊 我好开心呀。

2019-08-17

这个世界会好的。我们也会好的。

Posted on

明晚来更新，不然这周不喝可乐了！

2018-11-20,这周没有可乐喝了。。。sad

不过今天了解了下序列化和反序列化的东西，后面写出来一下

zhangyang chishibani!

Posted on

瀑布的水逆流而上，
蒲公英的种子从远处飘回，聚成伞的模样，
太阳从西边升起，落向东方。
子弹退回枪膛，
运动员回到起跑线山，
我交回录取通知书，忘了十年寒窗。
厨房里飘来饭菜的香，
你把我的卷子签好名字，
关掉电视，帮我把书包背上。
你还在我身旁。

Posted on

思考的代价

人类大脑在变得越来越大的过程中，使智人更倾向于直立行走，也改变了女性的怀孕时间，人类都是早产儿（那剖腹产算什么？）
相较之下，人类转眼登上顶端，不仅让生态系统猝不及防，也让人类不知所措。
人类历史上的众多灾难，不论是生灵涂炭的战乱还是生态遭逢的浩劫，其实都是源于这场过于仓促的跳跃。

我们在生活学习中面对巨大的跳跃的时候，还是应当稳健稳健，毕竟我们是个体，是我们自己意志主导的~ 同时我们的不起眼的习惯，里面可能有大文章

替代理论

类似于美洲大陆被欧洲人发现时的印第安人大屠杀，历史上智人也许对尼安德特人挥起了屠刀。
纳粹

人际交往的限制

社会研究指出，根据八卦来维持的最大’自然’团体就是150人。只要超过这个数字，大多数人就无法真正深入了解，八卦所有成员的生活情形。

我也觉得的太多的交际反而让我感到不安
不过随着移动互联网的发展 ，改善了我们的交流方式，这个数字应该不止150人，但是face to face来的感情才是最真的！

我们的智力

讨论虚构的事物，是人类特有的能力
叫拉布拉多来算微积分？，不如让它来泼墨吧！

新旧之别

书中观点认为虽然我们现代人的知识量可谓是碾压采集时代的人，但是就单体所掌握的来说，现代人是比不上古人的。其理由在于那个时代的人们需要求生而掌握的知识和技巧远远多于现代人，例如他们需要知道动植物的习性，需要明白地形天气，也要知道怎么走怎么运动才是最省力的等等（PS:他们的身体素质也应该远超过绝大多数的现代人）。不过我认为这就是进化的好处，在之前智人因为语言等文化称霸了人类，于是这也就是成了我们的进化方向，我必须承认绝大多数的我们都是普通的人，没有超乎常人的智力，但是我们可以通过合作达成’1+1>2’的效果，我们现在不需要个人你掌握很多很多的东西，Team Work可以创造更多。

书中还提到了幸福感的问题，作者的观点认为是采集时代的智人会比现在更加幸福，因为没有这么多的压力疾病之类的。虽然也很有道理，但是我认为幸福永远是我们自己的事，应当自己去追求的，比谁更幸福真心没用。

宗教

在远古时期的人类是相信泛神论（各种宗教，图腾，邪教之类的）的，他们认为万物有灵（拉丁语中’anima’既是’灵魂’意思），再普通不过的石头小草都是有灵性的，这一点上，现在世界的绝大多数教派都达成了共识，我会觉得很神奇，为什么当时还几乎没有任何联系的会在上面达成让人惊讶的一致，我猜应该是我们基因决定的吧，再多的不同，可是我们终究发源于同一个地方，生活在同一片天空之下。不过作为一名还比较坚定的无神论者 待续

关于生态

人类造成了世界上绝大所数生物的灭绝 ，在向其他陆地进发的时候，作为狩猎者的人类可谓是见神杀神见佛杀佛，无所不用其极，能好怎用得是出神入化。

小麦驯化了智人

智人由采集的生活转换为农业，限制了自己的活动空间，改变了自己做的事情，换个角度想来，说智人驯化了人类也没错。

关于历史

在现代晚期之前，总人口有九成以上都是农民，日出而作，日落而息。他们生产出的粮食养活了一小撮的精英分子：国王，官员，战士，艺术家，思想家，科学家，但历史写的几乎全是这些人的故事。于是历史只告诉了我们极少数的人在作什么，而其他绝大多数人的生活就是不停地跳水耕田。

我认为这是理所应当的，大自然的法则便是优胜劣汰，但莫要成为那种精致的利己主义者就好，享受了资源，便理所应当地付出。艺术家给人精神享受，思想家带给我们不同的精神世界，科学家去探索世界的真相，政府机构组织起了庞大的人类社会等等等…

秩序

现代我们社会的秩序其实来源于人类极致的想象能力，最有名的比如美国的《独立宣言》，’联合国’等。秩序由人类制定，但也得由人类接受才能有效。
我接受的教育是人人平等，但先天的影响与后天的作为着实是不平等的

历史从无正义

在我读完看来，其实男女是平等的，历史上的人做了符合当时情况的选择，也就是最大似然估计。在面对战争,生产,甚至某些创作的时候，大多数情况下所表现出来的能力优于女性，于是被选择了。若不信可以试试，假设有一个国家，其女性的决定性的能力高于男性，那发展100年或者更久之后，这个国家会不会就是现在大多数国家的镜像，只不过男女颠倒而已。再加一点，上个世纪开始的关于女性人权的讨论，大多数不也是那些能力卓越的女性所领导的。所以这并不是男女的区别，而是能力的问题。
我还是坚决支持男女平等的，公平竞争多好啊

关于历史的融合与统一

曾经读到一本书，大意是：“人类发展到最后必然走向统一，且在无比巨大的人口基数下，帝国是最好的方式”。这类的问题我没有过多的思考过，不过我想我最应该注意的是自己的生活，如果能够和家人幸福地生活下去，那其他的又有什么重要？

Money

金钱是有史以来最普遍也是最有效的互信系统。

关于帝国

2200年前的今天，也许我的祖先还被人称做‘蛮子’，可是现在他的子孙也被叫做汉人。我们应该这么安慰自己：我们只是时间长河上一滴水，大家一起打出其中的一些水花便被蒸发，可是百川入海。PS：我也不知道我写的这句话有什么意思..

资本主义

是人类的自私与懒惰促进了现代的发展？

Posted on

导语

Markdown写习惯了看起来还是习惯很多。

安装

安装之类的十分简单，毕竟是轻量级的标记语言（以下仅推荐）。

  • Windows: MarkdownPad
  • IOS: Mou
  • Web: 简书
  • Linux: Sublime Text 3

语法

  1. 标题
    一般使用Atx形式

    red

    red

    red
    code:  
 ###red  
 ####red  
 #####red
  2. 列表
    • 有序列表
      1. red
      2. blue
        数字序列+英文.+一个空格
    • 无序列表 
       + red   
 - blue  
 * yellow
  3. 引用
    使用>符号，在句子的最开始处

岂曰无衣 与子同袍

  1. 代码区块
    使用连续三` 来标记，eg: 
     print(Hello Markdown)  

    code:  
```print(Hello Markdown)
    `` 或者是使用tab`键，四个缩进即可

  2. 分隔线 

    code:  
 ---  
 ***
  3. 换行
    在换行处先敲两个空格再回车即可
  4. 链接 
          code:  
              I love [google][1] ,not [baidu][2]  
              [1]:www.google.com
              [2]:www.baidu.com
  1. 强调
    使用*或者_来标记
    山随平野尽，江入大荒流
    七月在野，八月在宇，九月在户，十月蟋蟀,入我床下
      code:
       **山随平野尽，江入大荒流**    
        *七月在野，八月在宇，九月在户，十月蟋蟀,入我床下*
  2. 图片
    方法类似于链接

其实这个语法真的蛮简单的，排版出来也工整漂亮，hhh ~
友情提示：Web版和客户端版的解码有问题。所以最好别换着换着编辑,别问我怎么知道的。。昨晚眼睛有快写瞎了,今天打开一看，WCNMLGBD乱码=重写 　　

以上，hiahia
这里是我学习的Markdown的地方。